Представление информации в компьютерах

Информация в ЦВМ представляется в кодированном виде, а именно в виде последовательности цифр, т.е. чисел. При этом это может быть либо собственно числа со знаком либо символы - числа без знака.

Числа в ЦВМ представляется не в десятичной системе счисления, а в двоичной, т.е. в каждой разрядной позиции может быть не 10 различных символов, а 2: "0" и "1".

Такое представление вызвано техническими соображениями:

двухстабильный элемент создать легче, чем 10-и. Примеры двустабильных элементов: чёрное - белое; высокий - низкий; наличие - отсутствие, истинно - ложно.

2.2. Основы алгебры логики.

Двоичная система оказалась очень удобной для построения элементной базы ЦВМ, поскольку оказалось возможным использовать аппарат математической логики, базирующейся на том, что любое суждение (утверждение) является двоичным: истинное и ложное. Двоичная алгебра была создана Джоном Булем ("Математический анализ логики" 1847г.), которая получила название булевой алгебры.

Для описания функционирования цифровых схем используется математический аппарат булевых функций (части функций алгебры логики). ФАЛ, как и ее переменные, могут принимать только два значения.

Особый интерес представляют булевы функции одной и двух перемен. Функции для большего числа переменных могут быть сведены к функциям от двух переменных.

Количество функций одной переменной равно 22 = 4

Аргумент	Функция	Обозначение	Название
х	Значение	F(x
0 1	0 0	F0(х)	Константа «0»
0 1	0 1	F1(x)	Переменная «х»
0 1	1 0	F2(x)	Отрицание (инверсия) «/х»
0 1	1 1	F3(x)	Константа «1»

<






Количество функций двух переменных (22)2 = 16

Аргумент	Функции
X	Y	F0	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15
0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
0	1	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
1	0	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
1	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1

     f0 - константа 0

     F1 - x&y конъюнкция (*, , /\)

F2 - хÌ`y запрет по у - отрицание импликации х`y

F3 - х - переменная х

       F4     xÌy - запрет по х - отрицание импликации `xy

     F5 - у

     F6 - x?y - неэквивалентность             x`y\/`xy

     F7 - x\/y -   дизъюнкция (+)

     F8 - x|y - стрелка Пирса                   x\/y -не-или

                                                                    _ _

     F9 - x=y эквивалентность                   xy\/xy

                                                                      _

   F10- y - не у                                            y

                                                                    _

     F11 - yÌx импликация от у к х            y\/x



     F12 - x - не х

                                                                      _

     F13 - xÌy импликация от х к у             x\/y

                                                                  ___

     F14 - x/y - штрих Шеффера               хy - не и

     F15 - 1



     Система булевых функций является функционально полной, если любую булеву функцию можно представить посредством этой системы.

     Так можно доказать что любое сложное высказывание может быть выражено в виде формулы, в которой используются только три операции:

конъюнкция, дизъюнкция и отрицание. Будем их обозначать символами: отсутствие символа, «+» и «`   »

Аксиомы алгебры логики.

                                                _               _

     00 = 0 ;      1+1 = 1;           0 = 1:       1 = 0;



     А+0 = А:    А1 = А;           А+1 = 1   А0 = 0        А+А = А   АА = А

    ___   _                            _           _

    (А) = А; (А) = А;     А+А = 1;   АА = 0;



             Теорема де Моргана.

       ___      _ _      __      _    _

      А+В = А В;    АВ = А + В



                   Законы алгебры логики.



     Для такой алгебры справедливы законы

       а) коммутативности:     АВ=ВА          А+В=В+А

       б) ассоциативности:     А(ВС)=(АВ)С ;      А+(В+С) = (А+В)+С

       в) дистрибутивности: А(В+С) = АВ+АС;     А+ВС = (А+В)(А+С)

       г) поглощения:             А(А+В) = А;    А + АВ = А ;



      Таблицы булевых операций   двух переменных



Дизьюнкция                                                Конъюнкция

                  _         _

Х	У	Х+У
0	0	0
0	1	1
1	0	1
1	1	1

Х	У	ХУ
0	0	0
0	1	0
1	0	0
1	1	1

F=ХУ+ХУ+ХУ=Х+У F= ХУ

_       _    _ _       ____

F=`ХУ = ХУ = Х+У

                                                            _        _   _         _   ___

F=`ХУ+ХУ+ХУ=ХУ





При этом, как мы видим, существует две нормальные формы представления: дизъюнктивная (дизъюнкция конъюнкций) и конъюнктивная (конъюнкция дизъюнкций).

Можно показать, что функционально полной являются системы, состоящие из дизъюнкции и отрицания, из конъюнкции и отрицания, стрелка Пирса и штрих Шеффера.

2.3. Методы физического представления двоичных кодов.

     Различают два основных способа представления кодированной информации; параллельный код, (когда все биты предаются одновременно) и последовательный (когда биты передаются поочерёдно).

     Поскольку эти способы имеют противоположные требования к быстродействию и затратам оборудования, то применяют параллельно-последовательный способ.

     Напомним, что в ЦВТ информация подразделяется на биты, совокупности битов(байты, слова, и т.д.) и массивы (файлы, записи).

     Для идентификации отдельных элементов информации применяют специальные синхронизирующие сигналы или стробы.   По виду представления различают потенциальный вид и импульсный.

     При любых передачах параллельным кодом обычно применяют потенциальный способ представления информации, при этом стробирование осуществляется либо импульсом, либо фронтом, либо спадом.

Передачи последовательным кодом отличаются большим разнообразием способов кодирования: потенциальный, импульсный, кодирование направлением перепада (фазоманипулированный код), без стробирования (на фиксированной частоте).

Синхросигналы

Двоичный код 0 0 1 1 1 0 0 0

Потенциальный код

(без возврата к нулю

Импульсный код

Биполярный код

Фазоманипулир.

"Манчестер 2" - нули и единицы передаются разными фронтами

При параллельной передаче для идентификации отдельных элементов (байтов, слов) информации применяют специальные синхронизирующие сигналы или стробы. При этом различают синхронную и асинхронную

Синхронная передача

ТИ

Строб

подтверждения

Время удержания

строба данных

Время опережения

данными строба

Данные

Строб

данных

Асинхронная передача

Отмеченные выше средства кодирования цифровой информации являются средствами амплитудной модуляции (потенциалы, импульсы и фронты импульсов). Хотя средств кодирования существует бесконечное множество, отметим здесь средства кодирования посредством модуляции сигнала.

-       частотная: 0 и 1 – разными частотами;

-       фазовая: частота постоянная, но при переходе с 0 на 1 меняется фаза сигнала.

.

2.4. Схемная (физическая) реализация логических функций.

Основные параметры логических элементов.

     - технология изготовления

     - задержка распространения (частота переключения)

     - мощность потребления

     - нагрузочная способность (количество себе подобных)

Наиболее просто проиллюстрировать реализацию логических функций на основе транзисторной логики.

+ + +

xy xy

`х

х х

НЕ

и-не

Время удержания

данных

         +                                          +

x+y x+y

или

или-не

  Приведенные схемы являются комбинационными, то есть значение выходного сигнала однозначно определяется входными сигналами. Кстати, приведенные схемы реализуют положительную логику, когда логической единице соответствует более высокий уровень, если же принять за логическую единицу более низкий уровень, то операции "и" и "или" поменяются местами.



2.4.3. Комбинационные схемы

              Таблица истинности одного разряда двоичного сумматора.

x	y	c	S	Co
0	0	0	0	0
1	0	0	1	0
0	1	0	1	0
1	1	0	0	1
0	0	1	1	0
1	0	1	0	1
0	1	1	0	1
1	1	1	1	1

S = x`y`c+ `xy`c+xy`c+xyc

Co= xy`c + x`yc +`xyc +xyc





2.6. Элементы с памятью.

Элемент двоичного хранения (триггер) на элементах «или-не». . Это уже не комбинационная схема, а последовательностная (конечный автомат) – схема с памятью.

Работа логических элементов описывается и с помощью временных диаграмм.

S `Qn+1

Qn

         _                                                                                            `Q

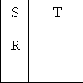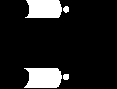
         Qn

                   R                          Qn+1

1    2           3       4         5             6    7      8    9

S

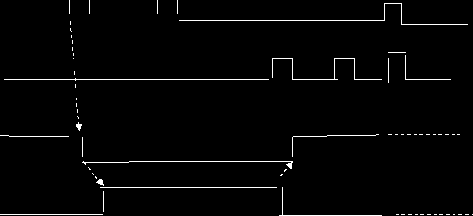
R

_

Q

Q



             Таблица переходов асинхронного R-S триггера.

Значение его выходного сигнала зависит не только от значений входных сигналов, но и от его внутреннего состояния.

№	R	S	Qn	Q(n+1)	Состояние
1	0	0	0	0	хранение "0"
2	0	1	0	1	установка в "1"
3	0	0	1	1	хранение "1"
4	0	1	1	1	хранение "1"
5	0	0	1	1	хранение "1"
6	1	0	1	0	установка в "0"
7	0	0	0	0	хранение "0"
8	1	0	0	0	хранение "0"
9	1	1	0	х	недопустимо
10	1	1	1	х	недопустимо

<

             Синхронный R-S триггер

   Синхронный R- S триггер получается из асинхронного триггера путем добавления по И ко входам R и S дополнительного входа С.

s T

c

R

                   D –триггер

                   Мы уже обратили внимание, что одновременная подача сигналов на входы S и R недопустима. Чтобы это исключить можно договориться, чтобы эти сигналы были инверсные друг другу, т.е. заменить их одним сигналом тогда получаем cсинхронный D триггер



   Синхронный D триггер

C	D	Qn	Qn+1	Функция
0	0	0	0	хранение "0"
0	0	1	1	хранение "1"
0	1	0	0	хранение "0"
0	1	1	1	хранение "1"
1	0	0	0	хранение "0"
1	0	1	0	установка в"0"
1	1	0	1	установка в"1"
1	1	1	1	хранение "1"

          _

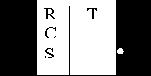
          А



           А

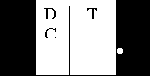   Различают D триггеры, запись в которые происходит по уровню, т.е.

в момент действия синхроимпульса триггер предcтавляет собой комбина-

ционную схему (триггеры типа защелки) и D-триггеры, запись в которые

происходит по фронту сигнала (переднему или заднему).



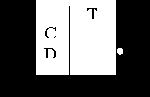
Cинхронный T триггер

     Если в качестве D-входа использовать инверсный выход самого триггера.

C	Qn	Qn+1	Функция
0	0	0	хранение "0"
1	0	1	установка "1"
0	1	1	хранение "1"
1	1	0	установка "0"

Из временной диаграммы можно сделать следующие выводы:

- частота на выходе в двое ниже частоты на входе

- элемент является сумматором по модулю 2, т.е. счетным элементом.

Совокупность синхронных триггеров, соединённых последовательно (выходы предшествующих на входы последующих, в том числе последнего с первым ) и общим сигналом на входах «С» образует регистр последовательного хранения (сдвига). Если же имеется соединение по только по входам «С», то получаем регистр параллельного хранения и параллельной передачи. Последовательное соединение Т-триггеров образует счётчик.

Содержание раздела