Формат чисел с плавающей точкой
Такая форма представления чисел, когда запятая размещается в определённом месте разрядной сетки, называется естественной (с фиксированной запятой).
Вообще говоря, числа в естественной форме могут быть смешанными
-248,3842
Смешанные числа могут иметь несколько представлений:
-0,2483842*103
\ \
мантисса порядок
или
-2,483842*102 или -0,02483842*104 или -24838,42*10-2
Такая форма представления носит название представления чисел с
Плавающей точкой, а сами числа называются вещественными..
|
Знак порядка |
Порядок |
Знак мантиссы |
Мантисса |
Обычно числа с плавающей запятой представляют в нормализованном виде. Условие нормализации: 0,1<=¦M¦<1. Таким образом формула представления вещественных чисел N = ±M*2±p
Пример.
Мантисса (дробная часть): три разряда и знак, экспонента (или порядок): два разряда и знак.
1. Отрицательные числа меньше -0,999х1099 - отрицательное переполнение
2. Отрицательные числа от -0,999х1099 до -0,100х10-99 - выражаемые отрицательные числа
3. Отрицательные числа от -0,100х10-99 до нуля - отрицательная потеря значимости.
4. Нуль.
5. Положительные числа от нуля до 0,100х10-99 - положительная потеря значимости.
6. Положительные числа от 0,100х10-99 до 0,999х1099 выражаемые положительные числа
7. Положительные числа больше 0,999х1099 - положительное переполнение.
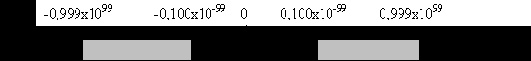 |
Действия над числами с плавающей запятой выполняются отдельно для порядков и мантисс. При операциях сложения (вычитания) требуется выравнивание порядков.
Сложение и вычитание.
1. Если порядки равны, выполнить операцию над мантиссами и нормализовать результат.
2. Иначе установить порядок результата равный большему.
3. Из большего порядка вычесть меньший.
4. Мантиссу операнда с меньшим порядком сдвинуть вправо на величину полученной разницы.
5. Сложить (вычесть) мантиссы и нормализовать результат.
Возможно переполнение как порядков так и мантисс.
При выполнении операций умножения (деления) порядки складываются (вычитаются). действия над мантиссами выполняются по правилам операций с фиксированной запятой.
Стандарт IEEE формата с плавающей запятой.
|
Знак мантиссы |
Смещённый порядок |
Мантисса |
Смещение = 2к-1-1, где к – разрядность поля порядка.
Таким образом, положительные числа (к=8, смещение = 127) от 0 до 255 превращаются в числа со знаком от –127 до +128.
|
Отр.область |
Пол.область |
||||
|
Обл. п-п |
Числа |
Потеря значимости |
Потеря значимости |
Числа |
Обл.п-п. |
|
(1-2-24)х2128 -0,5х2-127 0 0,5х2-127 (1- 2-24)х2128 |
|||||
2. Все единицы в поле порядка и ненулевое поле мантиссы – «не числа» («NaN»).
3. Крайние значения в поле порядка (все нули и все единицы) - особые величины.
4. Прочие значения в поле порядков используются для представления нормализованных чисел.
5. Старший разряд нормализованной мантиссы подразумевается.
6. Нули в поле порядков и в поле мантиссы +0 или - 0, в зависимости от знака мантиссы.
7. Все единицы в поле порядков с нулём в мантиссе + ? или -?.
8. Нулевое поле порядка с ненулевым полем мантиссы – ненормализованные числа: значение порядка минус 126 и неявный разряд мантиссы равен 0.
9. Все единицы в поле порядка и ненулевое поле мантиссы – «не числа» («NaN»).
Операции с плавающей запятой.
Сложение и вычитание было описано выше.
Умножение
1. Сложить порядки и из результата вычесть 127
2. Перемножить мантиссы и нормализовать результат.
Деление.
1. Вычесть порядок делителя из порядка делимого и прибавить 127.
2. Разделить мантиссы и нормализовать результат.
Кроме кодирования собственно числовой информации требуется и кодирование символов (букв различных алфавитов, математических символов и т.д.)Основополагающим является ASCII – стандартный американский код для обмена информацией – 128 символов (7 бит). Расширение обеспечивается с помощью кодовых страниц (с программным отслеживанием) – 256 символов (байт). Наконец, наиболее совершенным является UNICODE – 65536 символов (два байта) разделены на зоны (латынь -336 символов, русский -256 и т.д.).